-
Coach Letter
Toggle More InfoOctober 1, 2022
Dear Math Team Coach/Sponsor:
We are now in the final planning stages for the 17th annual FGCU Invitational Mathematics Competition. The competition will be held on Monday, December 19th, 2022 at Florida Gulf Coast University's main campus.
For Math subjectsThere will be prizes for the top 15 finishers in each of the six individual subject tests - algebra 1, algebra 2, geometry, statistics, precalculus, and calculus. The top 5 teams will receive team trophies and medallions, and there will be sweepstakes trophies for the top 5 schools and door prizes.
Each student will receive a certificate of participation by mail. An answer guide to each exam will be provided to each coach at the conclusion of the testing.
We have set a $12.00 per student registration fee which covers the cost of a tee shirt for each student. Raffle tickets will be provided to each student during check-in. Tee shirts will be distributed after the awards ceremony. Free bus and other vehicle parking on campus will be available.The FGCU Math Club will provide ushers for the test venues and maintain an information desk at the check-in point. Directions to FGCU and a campus map are available here.We hope your school will be able to participate and encourage you to RSVP with registration information by December 5th at the latest. The detailed schedule, contest rules, and registration form are available from the contest home page. Please note that this year we are offering e-mail registration in order to facilitate the grading of exams in the limited time frame we have. We would appreciate your taking advantage of this method.
If you have any questions regarding registration or other details, please email Contest Co-Director, Dr. Jerry Ellis , or call (239) 590-7253.
-
Registration
Toggle More InfoProf. Jerry Ellis, Contest Director Florida Gulf Coast University College of Arts & Sciences 10501 FGCU Blvd South Ft. Myers, FL 33965-6565We would appreciate having all registration info ASAP and fees by no later than December 9th. Please estimate the number of tee shirts of each size for your contingent (S, M, L, XL) and include that information with your payment.
Also, please advise with your payement if any students will require disability accommodation and the nature of that accommodation. We will make every reasonable effort to comply. If your group needs assistance in arranging overnight accommodations, please contact jkellis@fgcu.edu by November 24.
By registering for the contest, schools acknowledge that the contest rules are understood and agreed to. -
Directions to FGCU
Toggle More InfoFROM THE NORTH: Take I-75 to Alico Road, exit east to Ben Hill Griffin Parkway, then go south to the main entrance at FGCU Blvd. Don't turn at the north entrance.
FROM THE SOUTH: Take I-75 to Corkscrew Road, exit east to Ben Hill Griffin Parkway (light at Publix), then go north to the main entrance at FGCU Blvd.
In either case, check with the attendant at the parking kiosk located 1/8 mile from the main entrance for parking instructions. Check-in for competitors is at Whitaker Hall, first floor, on the south side of the building (across from observatory) in the Telford gallery. Please park in Parking Lot #7 and take the walking bridge across the lake directly to Whitaker Hall. -
Dining Options
Toggle More InfoOn Campus (link to map)
All the other FGCU dining facilities will be closedName Location Open/Close Einstein Bros Bagels Cohen Center 7:00a - 4:00p Chick-Fil-A Cohen Center 9:00a - 8:00p BYOB at Howard Hall Howard Hall 11:00a - 4:00p Starbucks Library 7:00a - 9:00p The Marketplace at Howard Hall Howard Hall 8:00a - 5:00p Dunkin' Donuts Homes Hall 7:30a - 4:00p The Marketplace at The Link Howard Hall 8:00a - 4:00p 239 BURGER BAR Cohen Center 11:00a - 5:00p Brahma Sushi Cohen Center 10:00a - 6:00p Boar's Head Howard Hall 11:00a - 4:00p SoVi Dining Hall South Village 7:00a - 10:00p Boardwalk / Azul's Brewhouse North Lake Village 4:00p - 10:00p Off Campus
- Perkins - Publix Mall / Corner of Corkscrew Road and Ben Hill Griffin Blvd.
- McDonald's - Publix Mall / Corner of Corkscrew Road and Ben Hill Griffin Blvd.
- Beef O'Brady's - Publix Mall / Corner of Corkscrew Road and Ben Hill Griffin Blvd.
- Subway - Publix Mall / Corner of Corkscrew Road and Ben Hill Griffin Blvd.
- China Gourmet - Publix Mall / Corner of Corkscrew Road and Ben Hill Griffin Blvd.
- Amore Brick Oven Pizza - Gulf Coast Town Center / West side of Ben Hill Griffin Blvd. just south of Alico Rd.
- Aurelio's Pizza - Gulf Coast Town Center / West side of Ben Hill Griffin Blvd. just south of Alico Rd.
- Burger 21 - Gulf Coast Town Center / West side of Ben Hill Griffin Blvd. just south of Alico Rd.
- Famous Dave's BBQ - Gulf Coast Town Center / West side of Ben Hill Griffin Blvd. just south of Alico Rd.
- Fosters Grille - Gulf Coast Town Center / West side of Ben Hill Griffin Blvd. just south of Alico Rd.
- McDonalds - Gulf Coast Town Center / West side of Ben Hill Griffin Blvd. just south of Alico Rd.
- Moe's Southwestern Grill - Gulf Coast Town Center / West side of Ben Hill Griffin Blvd. just south of Alico Rd.
- Pita Pit - Gulf Coast Town Center / West side of Ben Hill Griffin Blvd. just south of Alico Rd.
- Pollo Tropical - Gulf Coast Town Center / West side of Ben Hill Griffin Blvd. just south of Alico Rd.
- Red Robin Gourmet Burgers - Gulf Coast Town Center / West side of Ben Hill Griffin Blvd. just south of Alico Rd.
- Tijuana Flatts - Gulf Coast Town Center / West side of Ben Hill Griffin Blvd. just south of Alico Rd.
- Chipotle - Gulf Coast Town Center / West side of Ben Hill Griffin Blvd. just south of Alico Rd.
- Chili's - Gulf Coast Town Center / West side of Ben Hill Griffin Blvd. just south of Alico Rd.
- All American Grille / West side of Ben Hill Griffin Blvd. just north of Corkscrew Rd.
- Ford's Garage / West side of Ben Hill Griffin Blvd. just north of Corkscrew Rd.
- French Deli / West side of Ben Hill Griffin Blvd. just north of Corkscrew Rd.
- Luna Pizza / West side of Ben Hill Griffin Blvd. just north of Corkscrew Rd.
- Luna Rosa Italian Grille / West side of Ben Hill Griffin Blvd. just north of Corkscrew Rd.
- Duffy's / Southeast corner of Ben Hill Griffin Blvd. @ Corkscrew Rd. (before gate to Stoneybrook)
-
Contest Rules
Toggle More InfoWe will follow current FAMAT rules for calculator usage -
NO CALCULATORS PERMITTED FOR ANY SUBJECT TESTS, INDIVIDUAL OR TEAM, EXCEPT STATISTICS
GRAPHING CALCULATORS MAY BE USED FOR THE INDIVIDUAL OR TEAM STATISTICS TESTSIt is the responsibility of each team's sponsor to make sure students are using calculators in accordance with these rules. Failure to comply may result in individual or team disqualification.
Scantrons will be provided. Students need to bring their own pencils. If students are involved in statistics or an open exam they are allowed to bring calculators. More information about calculator usage can be found on Schedule page.
Teams will be composed of four students for each exam. Only one team per school per test category, please !
No limit on number of students participating in individual rounds.
Results from Algebra 1 and Statistics will not count toward overall school scores, however individual and team awards will be given for both subject areas. The reason for this is that not every school is able to field a team in these areas, and those schools not doing so would be unfairly penalized in the overall standings.
Contest officials at their sole discretion may resolve any tie scores, adjudicate the interpretation of any test question, invalidate the scoring of any test question, determine the admissibility of any response to a test question, and take any action which in their judgment benefits the conduct of the math competition.
All appeals to the dispute judge must be initiated no later than 15 minutes after the test containing the disputed question(s) ends.
AWARDS
I.Individual Awards
a. Trophies for the top 15 places in each of the content area exams.
b. See Scoring Rubric for awarding of points.
II. Division (content area) Awards
a. A team trophy for the top 5 teams.
b. A medallion for each team member.
c. See Scoring Rubric for awarding of points.
d. Scores of each team member (maximum of 4) plus the team score during the team round will count towards the division award.
III. Overall School Award
a. Trophies for the top 5 schools.
b. T-scores for each of the 4 counted divisions (Geometry, Algebra 2, Precalculus, & Calculus) will be added together for the overall school award.
ELIGIBILITY FOR COMPETITION
Eligibility for Algebra 1, Geometry, Algebra 2, and Statistics is one year each. The chart below outlines the tests students enrolled in each course may take. In general, students are expected to take the test that corresponds to the current course they are enrolled in. Students may “test up” by competition in a division for which they have not taken. Students may never “test down” by taking a test corresponding to a course they have already passed.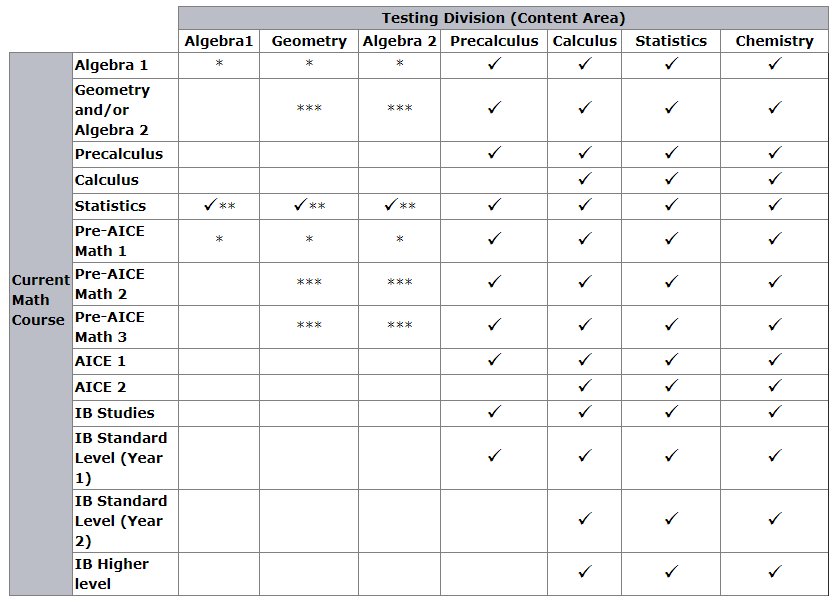
* Length of eligibility is 1 year for each of Algebra 1, 2, and Geometry, after which time the student will move to the next highest division.
** Students enrolled in Statistics and no other math class who have completed Algebra 2/Geometry, but no higher math class and never competed in Algebra 2/Geometry, may compete in Algebra 2/Geometry while enrolled in Statistics.
*** Any student enrolled in or having completed Algebra 2 and /or Geometry may compete in Algebra 2 or Geometry or both in the same year. However, there is a one-year eligibility in each division, and all other eligibility rules are still in effect. The same applies to Pre-AICE 2 and Pre-AICE 3.
-
Sponsors
Toggle More InfoCompetition was cancelled due Hurricane Irma.
-
Scoring Rubrics
Toggle More InfoScoring Room Supervisor: Prof. Rob Nichols
SCORING:
Scoring for the Individual Tests will be as follows:
1 points for each correct response
0 points for leaving the answer blank
0 point for answering incorrectlyScoring for the Team Round will be as follows:
16 points for getting question correct in the first minute
12 points for getting question correct in the second minute
8 points for getting question correct in the third minute
4 points for getting question correct in the fourth minute
0 points for getting question correct after time expiresTIES:
INDIVIDUAL TESTS:
All tie scores will be broken according to the following rules which apply to a given subject test:
(1) Any student who receives a score of N on the general round will be ranked above a student who receives a score of M if N>M, regardless of the outcome of any subsequent tie-breaking rounds.
(2) Any students achieving a perfect score during the general round will be deemed to be tied, and will participate in a tie-breaking round according to the procedure in (5) below.
(3) Any students achieving the same score other than in (2) during the general round and having done so by answering the identical questions correctly, will be deemed to be tied, and will participate in a tie-breaking round according to the procedure in (5) below.
(4) Any students achieving the same score other than in (2) during the general round, and having done so by answering a different set of questions correctly, will be deemed to have different ranking. The lower ranking will go to the student who misses the earlier question posed in the general round.
(5) Any students who are deemed to be tied will participate in a sudden death tie-breaker consisting of a supplemental round of questions comparable to the questions asked in the general round. At the sole discretion of the Scoring Room Supervisor, the tie-breaker round for a given subject test may be administered simultaneously to all students who are tied according to both (2) or (3) above. Students participating in a tie breaker round will simultaneously receive one question at a time, and have a fixed amount of time to respond in writing. Within a group of mutually tied students, any student missing a given question will be ranked below any other student not missing that question. A student whose ranking according to this procedure is definitely and irrefutably established will be excused from further participation in the round. The supplemental round will continue until all ties are broken.TEAM TESTS:
All tie scores will be broken according to the following rules which apply to a given subject test:
(1) Teams with the same overall score at the end of the team round will be ranked according to the individual scores constituting that overall score. More specifically, the individual scores for a team will be arranged from highest to lowest. The highest score will be considered the first score, the next highest score (possibly equal to the highest score) will be considered the second score, and so forth according to the obvious rule. The sequences of scores obtained in this manner from teams that are tied at a given overall score will be compared from first to last. Any team whose sequence of scores agrees with another team from the first to the Nth position, but whose N+1st score is lower than that of the other team, will be ranked below the team with the higher N+1st score.
(2) Teams with the same overall score at the end of the team round, and whose sequences of individual scores as defined in (1) of this section are the same, will participate in a team tie-breaker round. The procedure for the team tie-breaker round will be the same as for the individual tie-breaker round in (5) of the preceding section, with the word “team” substituted consistently for “student”.MISC:
Interpretation and application of the preceding rules, including the discretion to modify them to resolve unforeseen circumstances, is the sole prerogative of the Scoring Room Supervisor or Designee thereof.
-
Test Preparation Standards
Toggle More InfoTESTING STANDARDS
Algebra 1 (MAT 1033):
- Basic Concepts
- The Real Number System
- Operations with Real Numbers
- Powers, Square Roots, and the Order of Operations
- Integer Exponents and Scientific Notation
- Operations with Variables and Grouping Symbols
- Evaluating Variable Expressions and Formulas
- Linear Equations and Inequalities
- First-Degree Equations with One Unknown
- Literal Equations and Formulas
- Absolute Value Equations
- Using Equations to Solve Word Problems
- Solving More-Involved Word Problems
- Linear Inequalities
- Compound Inequalities
- Absolute Value Inequalities
III. Equations and Inequalities in Two Variables and Functions
- Graphing Linear Equations with Two Unknowns
- Slope of a Line
- Graphs and the Equations of a Line
- Linear Inequalities in Two Variables
- Concept of a Function
- Graphing Functions from Equations and Tables of Data
- Systems of Linear Equations and Inequalities
- Systems of Linear Equations in Two Variables
- Systems of Linear Equations in Three Variables
- Applications of Systems of Linear Equations
- Systems of Linear Inequalities
- Polynomials
- Introduction to Polynomials and Polynomial Functions: Adding, Subtracting, and Multiplying
- Dividing Polynomials
- Synthetic Division
- Removing Common Factors; Factoring by Grouping
- Factoring Trinomials
- Special Case Factoring
- Factoring a Polynomial Completely
- Solving Equations and Applications Using Polynomials
Geometry:
- Points, Lines, Planes, and Angles
- Points, Lines, and Planes
- Segments, Rays, and Distance
- Angles
- Postulates and Theorems Relating Points, Lines, and Planes
- Deductive Reasoning
- If-Then Statements; Converses
- Properties from Algebra
- Proving Theorems
- Special Pairs of Angles
- Perpendicular Lines
- Planning a Proof
III. Parallel Lines and Planes
- Definitions
- Properties of Parallel Lines
- Proving Lines Parallel
- Angles of a Triangle
- Angles of a Polygon
- Inductive Reasoning
- Congruent Triangles
- Congruent Figures
- Some Ways to Prove Triangles Congruent
- Using Congruent Triangles
- The Isosceles Triangle Theorems
- Other Methods of Proving Triangles Congruent
- Using More than One Pair of Congruent Triangles
- Medians, Altitudes, and Perpendicular Bisectors
- Quadrilaterals
- Properties of Parallelograms
- Ways to Prove that Quadrilaterals Are Parallelograms
- Theorems Involving Parallel Lines
- Special Parallelograms
- Trapezoids
- Inequalities in Geometry
- Inequalities
- Inverses and Contrapositives
- Indirect Proof
- Inequalities for One Triangle
- Inequalities for Two Triangles
VII. Similar Polygons
- Ratio and Proportion
- Properties of Proportions
- Similar Polygons
- A Postulate for Similar Triangles
- Theorems for Similar Triangles
- Proportional Lengths
VIII. Right Triangles
- Similarity in Right Triangles
- The Pythagorean Theorem
- The Converse of the Pythagorean Theorem
- Special Right Triangles
- The Tangent Ratio
- The Sine and Cosine Ratios
- Applications of Right Triangle Trigonometry
Algebra 2 (MAC 1105):
- Fundamental Concepts of Algebra
- Real Numbers and Algebraic Expressions
- Exponents and Scientific Notation
- Radicals and Rational Exponents
- Polynomials
- Factoring Polynomials
- Rational Expressions
- Equations, Inequalities, and Mathematical Models
- Graphs and Graphing Utilities
- Linear Equations
- Formulas and Applications
- Complex Numbers
- Quadratic Equations
- Other Types of Equations
- Linear Inequalities
- Quadratic and Rational Inequalities
III. Functions and Graphs
- Lines and Slope
- Distance and Midpoint Formulas; Circles
- Basics of Functions
- Graphs of Functions
- Transformations of Functions
- Combinations of Functions; Composite Functions
- Inverse Functions
- Polynomial and Rational Functions
- Quadratic Functions
- Polynomial Functions and Their Graphs
- Dividing Polynomials: Remainder and Factor Theorems
- Zeros of Polynomial Functions
- More on Zeros of Polynomial Functions
- Rational Functions and Their Graphs
- Modeling Using Variation
- Exponential and Logarithmic Functions
- Exponential Functions
- Logarithmic Functions
- Properties of Logarithms
- Exponential and Logarithmic Equations
- Modeling with Exponential and Logarithmic Functions
- Systems of Equations and Inequalities
- Systems of Linear Equations in Two Variables
- Systems of Linear Equations in Three Variables
- Partial Fractions
- Systems of Nonlinear Equations in Two Variables
- Systems of Inequalities
- Linear Programming
VII. Conic Sections and Analytic Geometry
- The Ellipse
- The Hyperbola
- The Parabola
Precalculus (MAC 1147):
- Functions and Graphs
- Graphs and Graphing Utilities
- Basics of Functions and Their Graphs
- More on Functions and Their Graphs
- Linear Functions and Slope
- More on Slope
- Transformations of Functions
- Combinations of Functions; Composite Functions
- Inverse Functions
- Distance and Midpoint Formulas; Circles
- Modeling with Functions
- Polynomial and Rational Functions
- Complex Numbers
- Quadratic Functions
- Polynomial Functions and Their Graphs
- Dividing Polynomials; Remainder and Factor Theorems
- Zeros of Polynomial Functions
- Rational Functions and Their Graphs
- Polynomial and Rational Inequalities
- Modeling Using Variation
III. Exponential and Logarithmic Functions
- Exponential Functions
- Logarithmic Functions
- Properties of Logarithms
- Exponential and Logarithmic Equations
- Exponential Growth and Decay: Modeling Data
- Trigonometric Functions
- Angles and Radian Measure
- Trigonometric Functions: The Unit Circle
- Right Triangle Trigonometry
- Trigonometric Functions of Any Angle
- Graphs of Sine and Cosine Functions
- Graphs of Other Trigonometric Functions
- Inverse Trigonometric Functions
- Applications of Trigonometric Functions
- Analytic Trigonometry
- Verifying Trigonometric Identities
- Sum and Difference Formulas
- Double-Angle, Power-Reducing, and Half-Angle Formulas
- Product-to-Sum and Sum-to-Product Formulas
- Trigonometric Equations
- Additional Topics in Trigonometry
- The Law of Sines
- The Law of Cosines
VII. Systems of Equations and Inequalities
- Systems of Linear Equations in Two Variables
- Systems of Linear Equations in Three Variables
- Partial Fractions
- Systems of Nonlinear Equations in Two Variables
- Systems of Inequalities
- Linear Programming
VIII. Matrices and Determinants
- Matrix Solutions to Linear Systems
- Inconsistent and Dependent Systems and Their Applications
- Matrix Operations and Their Applications
- Multiplicative Inverses of Matrices and Matrix Equations
- Determinants and Cramer’s Rule
- Conic Sections and Analytic Geometry
- The Ellipse
- The Hyperbola
- The Parabola
- Rotation of Axes
- Parametric Equations
Calculus (MAC 2311):
- Functions and Models
- Four Ways to Represent a Function
- Mathematical Models: A Catalog of Essential Functions
- New Functions from Old Functions
- Exponential Functions
- Inverse Functions and Logarithms
- Limits and Derivatives
- The Tangent and Velocity Problems
- The Limit of a Function
- Calculating Limits Using the Limit Laws
- The Precise Definition of a Limit
- Continuity
- Limits at Infinity; Horizontal Asymptotes
- Derivatives and Rates of Change
- The Derivative as a Function
III. Differentiation Rules
- Derivatives of Polynomials and Exponential Functions
- The Product and Quotient Rules
- Derivatives of Trigonometric Functions
- The Chain Rule
- Implicit Differentiation
- Derivatives of Logarithmic Functions
- Exponential Growth and Decay
- Related Rates
- Linear Approximations and Differentials
- Hyperbolic Functions
- Applications of Differentiation
- Maximum and Minimum Values
- The Mean Value Theorem
- Indeterminate Forms and l’Hospital’s Rule
- Summary of Curve Sketching
- Optimization Problems
- Newton’s Method
- Antiderivatives
- Integrals
- Areas and Distances
- The Definite Integral
- The Fundamental Theorem of Calculus
- Indefinite Integrals and the Net Change Theorem
- The Substitution Rule
- Applications of Integration
- Areas Between Curves
- Volumes
- Volumes by Cylindrical Shells
- Work
- Average Value of a Function
VII. Techniques of Integration
- Integration by Parts
- Trigonometric Integrals
- Trigonometric Substitution
- Integration of Rational Functions by Partial Fractions
- Strategy for Integration
- Approximate Integration
- Improper Integrals
Statistics (STA 2023)
- Getting Started
- What Is Statistics?
- Random Samples
- Introduction to Experimental Design
- Organizing Data
- Frequency Distributions, Histograms, and Related Topics
- Bar Graphs, Circle Graphs, and Time-Series Graphs
- Stem-and-Leaf Displays
III. Averages and Variation
- Measures of Central Tendency: Mode, Median, and Mean
- Measures of Variation
- Percentiles and Box-and Whisker Plots
- Correlation and Regression
- Scatter Diagrams and Linear Correlation
- Linear Regression and the Coefficient of Determination
- Elementary Probability Theory
- What is Probability?
- Some Probability Rules – Compound Events
- Tree Diagrams and Counting Techniques
- The Binomial Probability Distribution and Related Topics
- Introduction to Random Variables and Probability Distributions
- Binomial Probabilities
- Additional Properties of Binomial Distributions
VII. Normal Curves and Sampling Distributions
- Graphs of Normal Probability Distributions
- Standard Units and Areas Under the Standard Normal Distribution
- Areas Under Any Normal Curve
- Sampling Distributions
- The Central Limit Theorem
- Normal Approximation to the Binomial Distribution
-
Proctor Instructions
Toggle More Info
